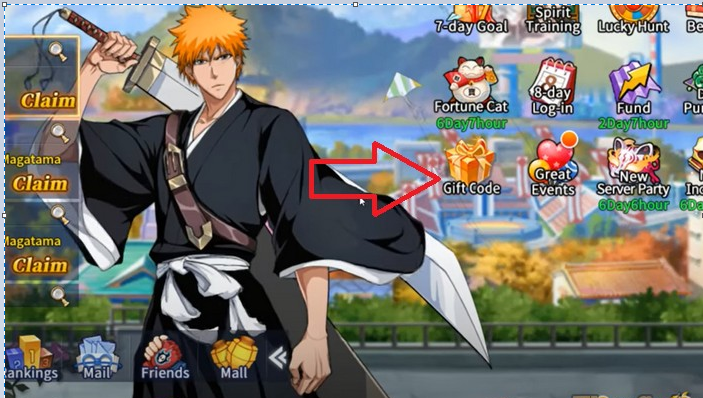
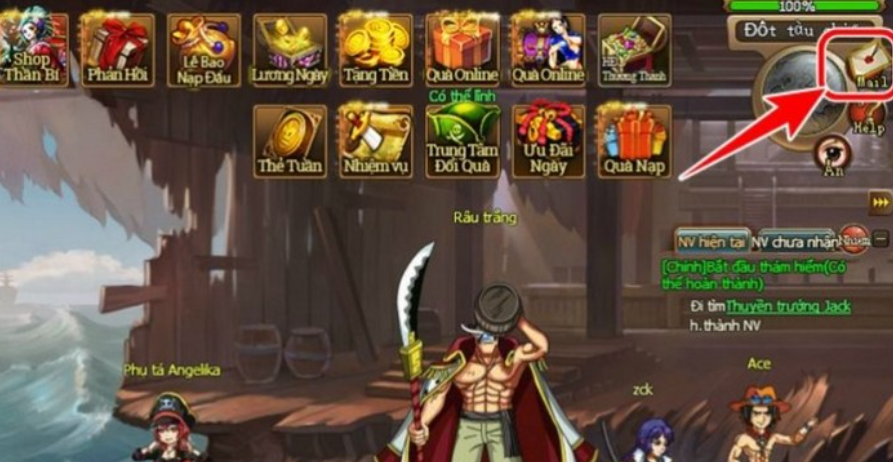
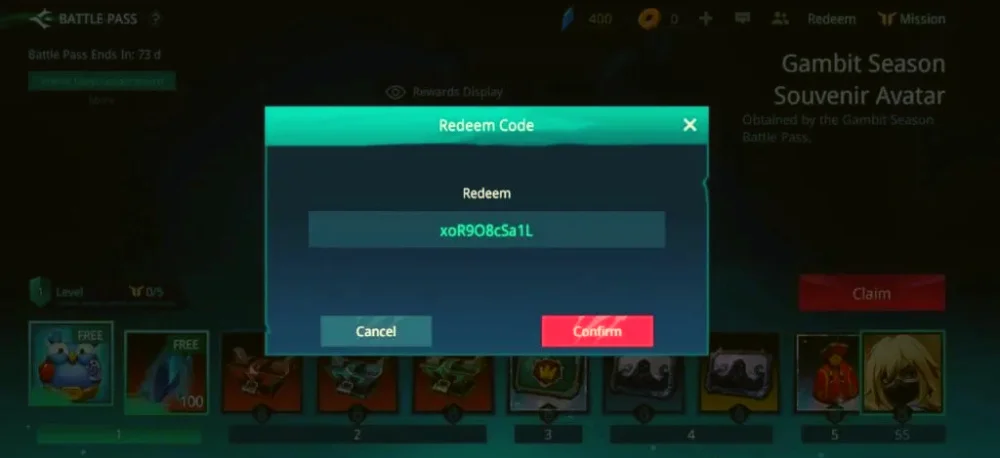
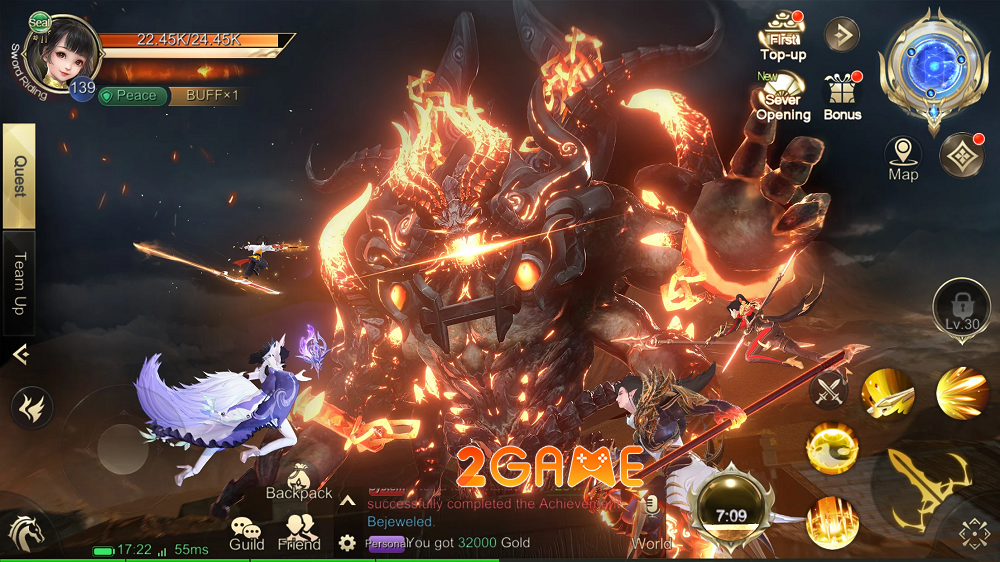
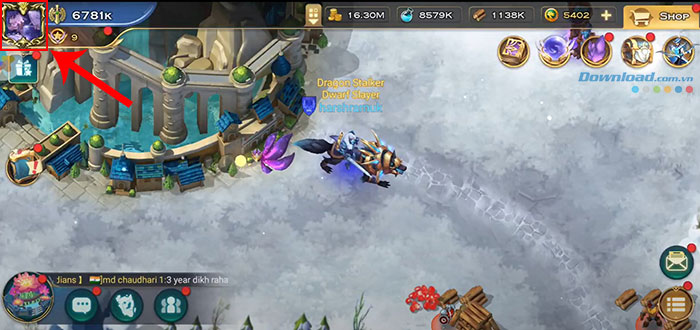
Bạn đã sẵn sàng khám phá danh sách mã code Bleach Huyết Chiến mới nhất năm 2023? Với những mã…
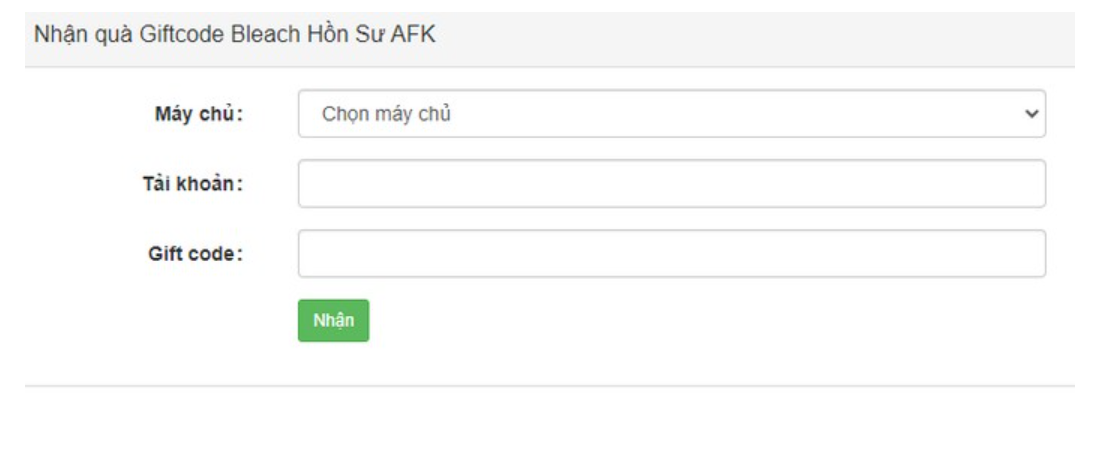
Bạn đã bao giờ muốn biết về các code bleach hồi sư AFK mới nhất năm 2023? Hãy cùng tienhieptruyenky…
Code Bleach Eternal Soul mới nhất năm 2023 đã chính thức ra mắt, vậy cách nhập code để nhận những…
Code Bleach Blood War mới nhất năm 2023, cách nhập code đã được tung ra! Hãy cùng khám phá ngay…
Trong bài viết này, chúng ta sẽ khám phá cách nhận toàn bộ mã code Blade of Pillar mới nhất.…
Bạn đã chơi BLACKPINK The Game và muốn biết cách thêm mã code blackpink the game mới nhất? Hãy cùng…
Bạn đang muốn khám phá cách nhận và nhập code Bitcoin Miner mới nhất? Tại đây, tôi đã tổng hợp…
Khám phá mã code Binh Pháp 37 Kế mới nhất năm 2023 và bước vào cuộc phiêu lưu thông qua những…
Bạn muốn tìm hiểu về mã code Big Lifting Simulator 2 mới nhất ? Hãy để tienhieptruyenky chia sẻ những…
Bạn muốn biết về các code Biệt Đội Đùn Đùn mới nhất tháng 8/2023? Hãy cùng tienhieptruyenky tìm hiểu và…
Bạn muốn khám phá code battle of monster mới nhất và biết cách nhập code battle of monster? Battle of…
Bạn đã bao giờ muốn trở thành một Elf mạnh mẽ trong Battle of Elf? Hãy khám phá cuộc phiêu…
Bạn đã có code battle night mới nhất chưa? Code battle night là một trò chơi thú vị dành cho…
Bạn muốn khám phá về code base battles mới nhất hay không? Code base battles là một cuộc thi thú…
Code bảo bối huyền thoại mới nhất là gì? Đây là một bí mật của game thẻ bài hấp dẫn…
Bạn đang muốn tìm hiểu về các mã Code Dị Giới 3Q mới nhất? Biệt Đội 3Q Mobile là một…
Bạn muốn biết mã Code Berry Avenue mới nhất hiện nay? Nếu bạn là một game thủ đang chơi tựa…
Bạn đang muốn khám phá các Code Bệnh Viện Kỳ Thú mới nhất? Trò chơi này cho phép người chơi…
Bạn đang tìm kiếm thông tin về code Bee Swarm Simulator mới nhất? Bee Swarm Simulator cho phép bạn trở…
Bạn muốn khám phá về các Code Beedom Mới Nhất? Beedom là một tựa game chiến lược thú vị với…
Bạn có đang chơi Be A Spider Tycoon trên Roblox và đang tìm kiếm mã Code Be A Spider Tycoon…
Bạn đang tìm kiếm về Code Bá Vương Đại Chiến mới nhất? Bá Vương Đại Chiến là một trò chơi…
Các mã Code Battle Through the Heavens mới nhất, hỗ trợ cho các game thủ đang chơi trò chơi này…
Bạn đang tìm hiểu về các Code Battle Storm Ninja Master mới nhất? Battle Storm Ninja Master là một trò…
Bạn đang tìm kiếm thông tin về Code Battle Storm: Nine Tails mới nhất? Battle Storm: Nine Tails là một…
Bạn đã từng muốn khám phá mã code bảo bối đại chiến mới nhất và biết cách nhập chúng vào…
Bạn đã từng muốn khám phá bí mật code Bản Năng Vô Cực 3D mới nhất? Với code này, bạn…
Bạn có muốn khám phá code bangbang origin mới nhất và biết cách nhập code bangbang origin không? Code bangbang…
Bạn muốn biết về code banana eats mới nhất và cách nhập code banana eats? Code banana eats là một…
Bạn muốn khám phá những Code Balls of Poke mới nhất và biết cách nhập chúng không? Code Balls of…
Bạn đang tìm kiếm một trò chơi hành động đỉnh cao? Đừng bỏ lỡ Badlanders – một thế giới tự…
Bạn có muốn tìm hiểu về mã code backrooms race clicker Mới Nhất và cách nhập code trong trò chơi…
Bắt kịp cơ hội nhận mã code Bạch Xà Tiên Kiếp Mobile mới nhất năm 2023! Đừng bỏ qua bài…
Hãy theo dõi bài viết này để khám phá cách nhập code Bạch Xà Tiên Kiếp Mới Nhất năm 2023.…
Bách Luyện Thành Thần là một tựa game di động hấp dẫn nhất trong năm 2023, được hàng loạt game…
Sau một thời gian dài chờ đợi, cuối cùng thì trò chơi Bách Kiếm Dạ Hành đã chính thức mở…
Bách Chiến 3Q là một trò chơi Tam Quốc chiến thuật với một phong cách hoàn toàn mới và độc…
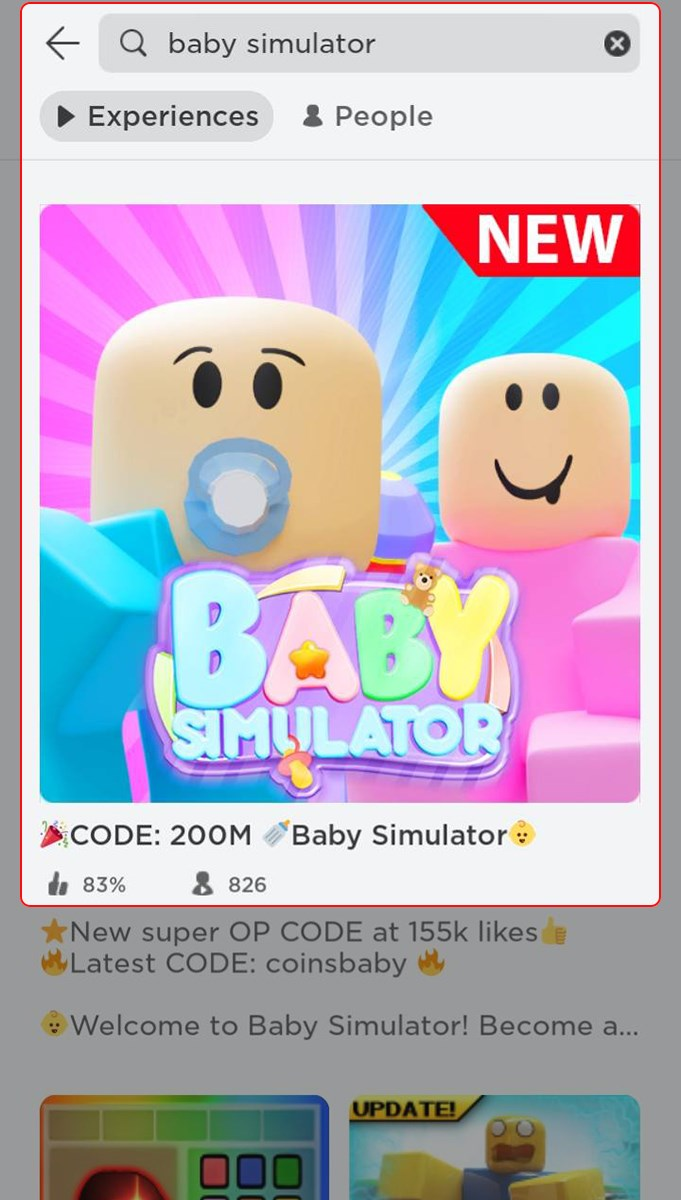
Baby Simulator là một trò chơi thú vị và hấp dẫn trong hệ thống game Roblox, ngoài ra còn có…
Bạn đang tìm kiếm các mã code awakening of the four emperors Mới Nhất đang hoạt động, hôm nay tienhieptruyenky…
Awaken Chaos Era là một tựa game nhập vai hấp dẫn được chơi trên điện thoại di động. Trong game,…
Bạn đang quan tâm đến AU TOP VTC Mobile và muốn biết về các mã Code Au Top mới nhất?…
Trong nội dung này, chúng tôi sẽ chia sẻ thông tin về code Auto Chess Moba mới nhất, cũng như…
Bạn đã bao giờ muốn nhận quà miễn phí trong trò chơi AU BEAT chưa? Code AU BEAT mới nhất…
Mã code Attack Simulator mới nhất đang khiến cộng đồng game thủ đứng ngồi không yên! Bài viết này sẽ…
Bạn muốn biết danh sách mã code Astral Lord Origin mới nhất và cách sử dụng? Chúng tôi đã thu…
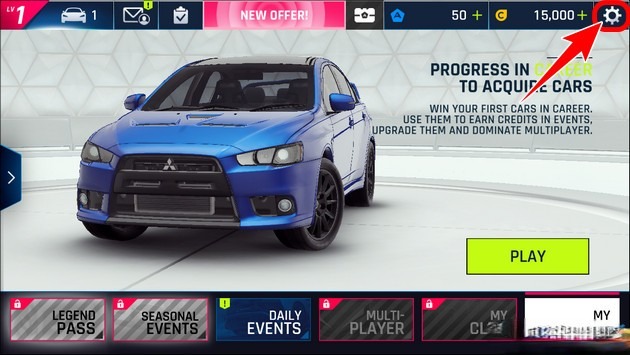
Bạn đã từng chơi Asphalt 9 Legends chưa? Đây là một tựa game đua xe vô cùng nổi tiếng với…
Bạn đã chơi Art of Conquest: Dark Horizon và muốn biết về các mã code Art of Conquest mới nhất…
Bạn đang chơi game Roblox và muốn biết mã code liên quan đến Arsenal? Đừng lo, tôi có tổng hợp…
Bạn đang chơi Army Control Simulator trên Roblox và muốn biết cách nhập mã code Army Control Simulator mới nhất…
Mời bạn tham gia vào trò chơi Arm Wrestle Simulator trên ROBLOX để có trải nghiệm tuyệt vời về tập…